허준이 교수에 필즈상 안긴 '조합 대수기하학'…어떤 난제 풀었나
조합 대수기하학, 사칙연산 바탕으로 기하학적 대상 연구
허준이 교수, 대수기하학 바탕으로 조합론 난제 다수 해결
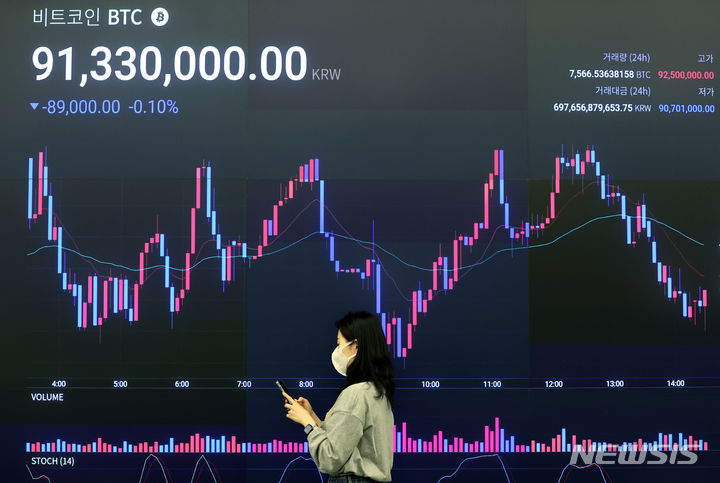
![[서울=뉴시스]허준이 프린스턴대 교수가 5일 핀란드 헬싱키에서 개최된 필즈상 시상식에서 상을 받고 있다. (사진=행사 중계 홈페이지 캡처) 2022.07.05](http://image.newsis.com/2022/07/05/NISI20220705_0001035061_web.jpg?rnd=20220705164952)
[서울=뉴시스]허준이 프린스턴대 교수가 5일 핀란드 헬싱키에서 개최된 필즈상 시상식에서 상을 받고 있다. (사진=행사 중계 홈페이지 캡처) 2022.07.05
[서울=뉴시스]윤현성 기자 = 허준이 미국 프린스턴대학교 교수 겸 한국고등과학원 석학교수가 한국계 수학자 역대 최초로 필즈상 수상의 영예를 안으면서 허 교수의 업적의 기반이 된 '조합 대수기하학'에도 관심이 쏠리고 있다.
5일 학계에 따르면 허 교수는 한국계 수학자 최초로 수학계 노벨상으로 여겨지는 필즈상을 수상했다. 필즈상은 국제수학연맹(IMU)이 4년마다 개최하는 세계수학자대회(ICM)에서 만 40세 미만 수학자에게 수여하는 수학계 최고의 상이다.
허 교수의 주 연구분야는 사칙연산을 바탕으로 기하학적인 대상을 연구하는 조합 대수기하학이다. 허 교수는 대수기하학을 바탕으로 조합론의 오래된 난제를 다수 해결하고 대수기하학의 새 지평을 연 공로를 인증받아 필즈상을 수상하게 됐다.
허 교수가 해결한 주요 난제 중 대표적인 것은 리드(Read) 추측과 호가(Hoggar) 추측이다.
일반적인 그래프의 채색다항식에 등장하는 계수들과 관련해 이 계수들이 '단봉 패턴'을 보인다는 가설이 리드 추측, '로그-오목성'을 가진다는 예상이 호가 추측이다. 허 교수는 이 추측들을 대수기하의 정리들을 이용해 해결해 수학 최고 학술지인 '미국수학회지(Journal of The American Mathematical Society)'에 출판했다.
그 이후에는 그래프를 일반화한 임의의 매트로이드에 대해서도 특성다항식의 계수들이 같은 로그-오목성을 만족한다는 훨씬 어려운 추측을 대수기하학에 등장하는 차우 환(Chow ring)의 조합적 정의 위에서 호지-리만 관계를 증명함으로써 규명해내기도 했다.
한편 이같은 허 교수의 업적은 비단 수학계 뿐만 아니라 산업 분야에도 지대한 영향을 미쳤다. 대한수학회에 따르면 허 교수의 연구 업적들은 정보통신, 반도체 설계, 교통, 물류, 기계학습, 통계물리 등 여러 응용 분야의 발달에 기여하고 있다.
◎공감언론 뉴시스 [email protected]
Copyright © NEWSIS.COM, 무단 전재 및 재배포 금지